Now that we know the 16 teams which advance from the group stage of the Champions League, we can compute the probabilities of the round of 16 match-ups.
It can get a little complicated, but don't worry – FFT has done the maths for you. Here is the table:
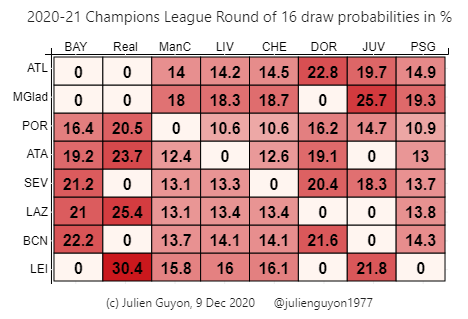
Borussia Monchengladbach happens to be the most likely opponent of Liverpool (18.3%), Manchester City (18%) and Chelsea (18.7%), the three English teams which remain in the competition. Porto, which Man City cannot meet again in the round of 16, is the least likely opponent of Liverpool and Chelsea (10.6%, least likely of all match-ups), while Atalanta is the least likely opponent of the Citizens (12.4%).
Overall, the most likely matchup is Real Madrid vs RB RB Leipzig, with more than 30% probability. The most likely opponent of Bayern Munich is Barcelona (there is a 22.2% chance that this final-like game will be the highlight of the round of 16). Reciprocity is by no means automatic: while Gladbach is the most likely opponent of the three English clubs, the most likely opponent for Gladbach is actually Juventus (25.7%). Notice that it is more likely than not (55%) that an English team will face Gladbach this winter.
One may wonder why Liverpool, Man City and Chelsea don't have the same probability 1/7 = 14.3% of meeting any of their seven possible opponents. One may also wonder why the probabilities vary so much, and how one could even compute them – we've explained in more depth previously.
MORE FROM THIS AUTHOR Champions League knockout draw: What if group winners could choose their opponents?
The group winners (written at the top of the table, in order from group A to group H) can only meet runners-up (listed on the left of the table, in the same order). However, a club cannot meet again the runner-up of its own group – hence the zeros on the diagonal. Moreover, two clubs from the same domestic league can't be drawn against each other: the off-diagonal zeros correspond to this constraint.
How can we compute all the non-zero probabilities? Let us take the example of Liverpool.
The Reds have seven possible opponents, so one could think that they have a 1/7 = 14.3% chance of meeting any of them. However, if we follow this reasoning, the probability of Liverpool vs Gladbach should also be 20%, since Gladbach only has five possible opponents. Of course, the probability of Liverpool vs Gladbach cannot be at the same time 14.3% and 20%. Actually, both numbers are wrong.
One may also be tempted to reason as follows. One lists all the admissible complete outcomes of the draw, that is, all the outcomes that satisfy all the constraints. This year, there are exactly 3,305 of them. Then, one measures the proportion of those 3,305 outcomes for which, say, Liverpool meet Gladbach. Since there are exactly 611 outcomes where Liverpool meet Gladbach, one would get a probability of 611/3305 = 18.5%.
However, this is not the correct probability either. It would be correct if UEFA drew one ball among 3,305, each ball representing an admissible complete outcome of the draw. But of course, this is not how the draw is done.
In order to calculate the true probabilities, you must pay attention to how exactly the draw is performed.
First, a runner-up is randomly drawn, and a (backtracking) algorithm determines the list of admissible opponents for the drawn team. This is not as simple as it looks, as the algorithm must prevent any future dead-end.
For instance, imagine that the two runners-up left to be drawn are Barcelona and Lazio, and the two remaining group winners are Real Madrid and Bayern Munich. If Lazio is drawn first, even though it can a priori play against both Real and Bayern, the computer will list Real as the only admissible opponent of Lazio, to make sure that the draw does not end up with Real vs Barça (forbidden since both teams are from Spain).
Once the list of admissible opponents is established, one of those opponents is randomly drawn. Then another runner-up is drawn, and the procedure repeats until all matchups are decided. This way, we avoid having to draw one ball among 3,305. But we also modify the draw probabilities!
A simple, robust way of computing the correct draw probabilities consists of simulating a very large number of complete draws, following the exact procedure followed by UEFA, and measuring the frequency of all the matchups. The above probability table was computed this way, after I simulated the draw a million times. It's also possible to calculate the exact probabilities on a computer. Both methods give the same results, up to the (very small) sampling error of the simulation method.
The draw procedure has an impact on the probabilities: Liverpool vs Gladbach is slightly less likely than it should be (18.3% vs 18.5%), whereas Chelsea vs Gladbach is slightly more likely than it should be (18.7% vs 18.5%). By 'should be', I mean if all of the 3,305 admissible outcomes of the draw were equally likely. And, as we showed here, drawing the group winners first, instead of the runners-up, would produce yet another set of probabilities.
To conclude, let us reflect on an intriguing fact: while Porto is the least likely opponent of Real, Real is the most likely opponent of Porto. Ah, when football invites us to reflect on probability and experience the wonder and beauty of mathematics!
Julien Guyon is a French mathematician and football fan. He is a quantitative analyst, and adjunct professor in the Department of Mathematics at Columbia University and at the Courant Institute of Mathematical Sciences, New York University. More probability tables are available on the author's Twitter accountand website.
While you’re here, subscribe to FourFourTwo and save 48% – available until Christmas. It’s the perfect gift idea for anybody who loves football (including yourself)!
NOW READ
IN THE MAG Robert Lewandowski voted Player of the Year in FourFourTwo Awards
INTERVIEW Jude Bellingham names the surprising Borussia Dortmund team-mate who stuns him in training
